Working with Data in R
Class #8 (Thu., Jan 30)
PDF version
Reading:
Required Reading (everyone):
- R for Data Science, Ch. 4–6.
Reading Notes:
Overview of the reading
- See the homework assignment for the exercises you whould do.
Chapter 4
This very short chapter goes over guidance on style for naming variables and functions and formatting your code to make it easy to read and keep it organized.
Chapter 5
This chapter introduces principles of tidy data and tools in R for organizing your data into tidy formats.
Principles of Tidy Data
The fundamental idea is that there are many ways to organize a data set in a table with rows and columns. Different kinds of analysis call for different ways of organizing your data. However, for all these ways of organizing, there is an overarching principle, illustrated in the figure below:
- Each variable is a column and each column is a variable
- Each observation is a row, and each row is an observation
- Each value is a cell and each cell is a value

Pivoting Data
The chapter has two principle parts, each of which focuses on a different aspect of pivoting data by rearranging rows and columns.
Lengthening Data
The first part looks at tools for lengthening data by combining many columns into a single column and adding another column to indicate what each row signifies.
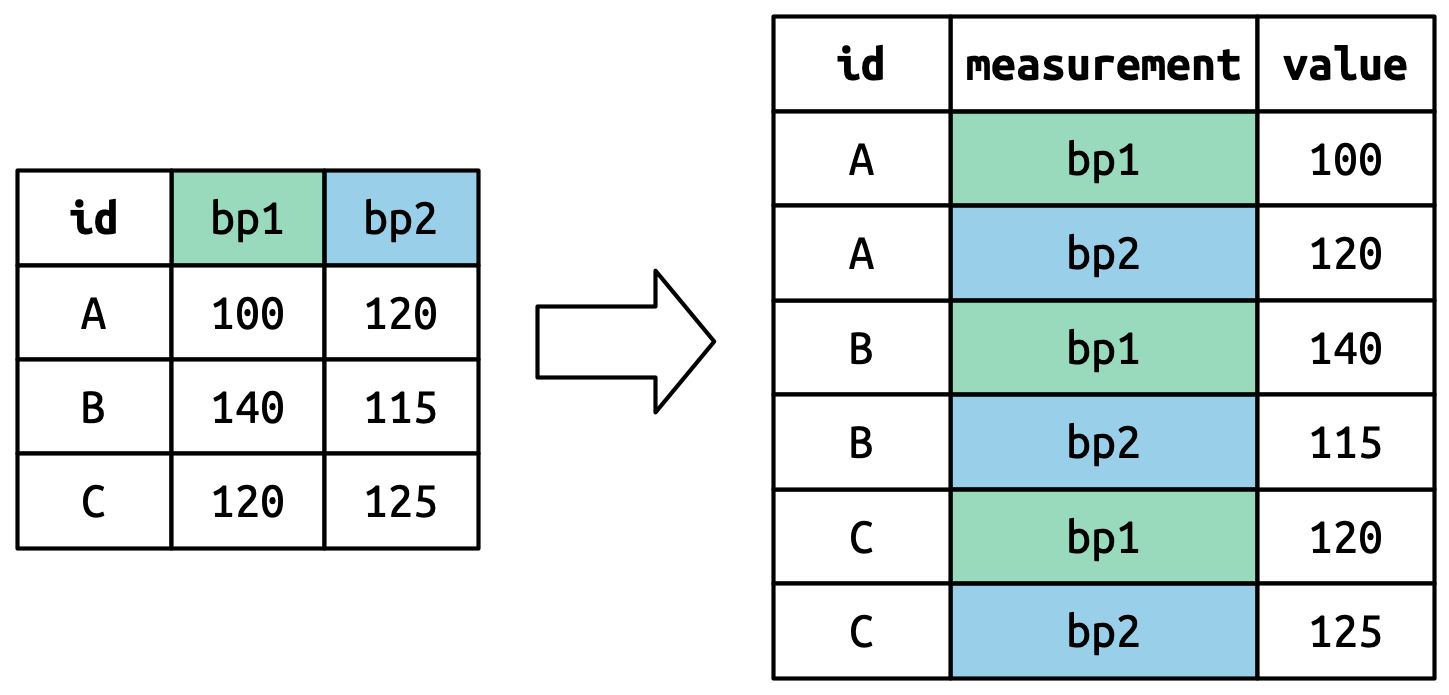
The key thing to pay attention to in this reading is the
pivot_longer() function. The distinct() function is also important,
because it helps us eliminate redundant rows.
Focus on sections 5.3.1 and 5.3.2.
Section 5.3.3 gets into fancier ways to lengthen data, which you will probably not need, so you can skim this section lightly.
However, do pay enough attention to section 5.3.3 that you will know what is possible and can return to it later if you’re reading in complicated data and need the more powerful tools to organize it.
Widening Data
The second part looks at tools for widening data by splitting up
one column into multiple columns. Widening is much simpler than
lengthening data, so this section is shorter. The key thing here
is to become familiar with the pivot_wider() function.
